Introduction
PGQL is a graph pattern-matching query language for the property graph data model. This document specifies the syntax and semantics of the language.
Changelog
The following are the changes since PGQL 1.1:
New features in PGQL 1.2
The new features are:
- Shortest path finding and Top-k shortest path finding.
- Scalar subqueries.
- ARRAY_AGG aggregation.
- ABS, CEIL/CEILING, FLOOR and ROUND math functions.
- EXTRACT function for extracting the
year/month/day/hour/minute/second/timezone_hour/timezone_minutefrom datetime values. - CASE statement.
- IN and NOT IN predicates.
Syntax changes in PGQL 1.2
PGQL 1.2 is a superset of PGQL 1.1. There are no changes to existing syntax other than additions.
A note on the Grammar
This document contains a complete grammar definition of PGQL, spread throughout the different sections. There is a single entry point into the grammar: Query.
Document Outline
- Introduction contains a changelog, a note on the grammar, and this outline.
- Graph Pattern Matching introduces the basic concepts of graph querying.
- Grouping and Aggregation describes the mechanism to group and aggregate results.
- Sorting and Row Limiting describes the ability to sort and paginate results.
- Variable-Length Paths introduces the constructs for testing for the existence of paths between pairs of vertices (i.e. “reachability testing”) as well as for retrieving shortest paths between pairs of vertices.
- Functions and Expressions describes the supported data types and corresponding functions and operations.
- Subqueries describes the syntax and semantics of subqueries for creating more complex queries that nest other queries.
- Other Syntactic rules describes additional syntactic rules that are not covered by the other sections, such as syntax for identifiers and comments.
Graph Pattern Matching
Property graph data model
A property graph has a name, which is a (character) string, and contains:
-
A set of vertices (or nodes).
- Each vertex has zero or more labels.
- Each vertex has zero or more properties (or attributes), which are arbitrary key-value pairs.
-
A set of edges (or relationships).
- Each edge is directed.
- Each edge has zero or more labels.
- Each edge has zero or more properties (or attributes), which are arbitrary key-value pairs.
Labels as well as names of properties are strings. Property values are scalars such as numerics, strings or booleans.
Example 1: Student Network
An example graph is:
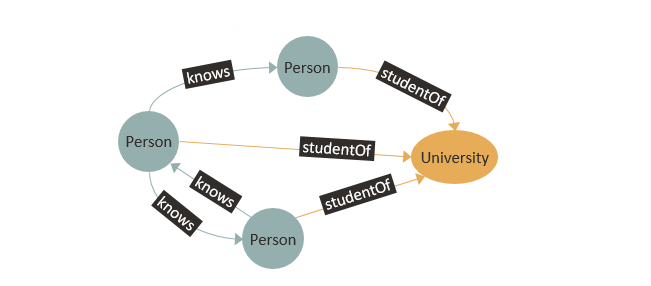
Here, student_network is the name of the graph. The graph has three vertices labeled Person and one vertex labeled University. There are six directed edges that connect the vertices. Three of them go from person to person vertices, and they have the label knows. Three others go from person to university vertices and are labeled studentOf. The person vertices have two properties, namely name for encoding the name of the person and dob for encoding the date of birth of the person. The university vertex has only a single property name for encoding the name of the university. The edges have no properties.
Example 2: Financial Transactions
An example graph with financial transactions is:
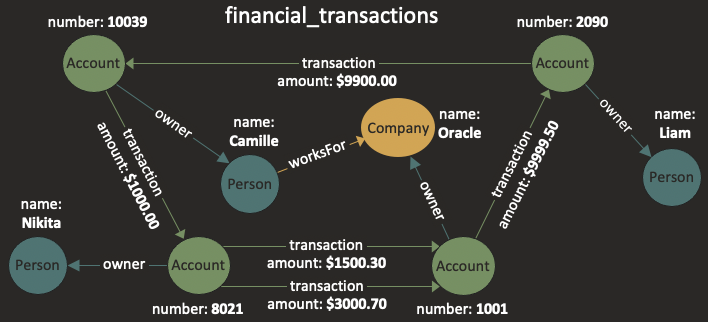
Here, financial_transactions is the name of the graph. The graph has three types of vertices. Vertices labeled Person or Company have a property name, while vertices labeled Account have a property number. There are edges labeled ownerOf from persons to accounts and from companies to accounts, and there are edges labeled transaction from accounts to accounts. Note that only the transaction edges have a property (amount).
Writing simple queries
This section is mostly example-based and is meant for beginning users.
Vertex patterns
The following query matches all the vertices with the label Person and retrieves their properties name and dob:

SELECT n.name, n.dob
FROM student_network
MATCH (n:Person)
+-----------------------+
| n.name | n.dob |
+-----------------------+
| Riya | 1995-03-20 |
| Kathrine | 1994-01-15 |
| Lee | 1996-01-29 |
+-----------------------+
In the query above:
student_networkis the name of the input graph.(n:Person)is a vertex pattern in whichnis a variable name and:Persona label expression.- Variable names like
ncan be freely chosen by the user. The vertices that match the pattern are said to “bind to the variable”. - The label expression
:Personspecifies that we match only vertices that have the labelPerson. n.nameandn.dobare property references.n.nameandn.dobaccess the propertiesnameanddobof the vertices that bind ton, respectively.
The query produces three results, which are returned as a table. The results are unordered.
Edge patterns
Edge patterns take the form of arrows like -[e]-> (match an outgoing edge) and <-[e]- (match an incoming edge).
For example:

SELECT a.name, b.name
FROM student_network
MATCH (a:Person) -[e:knows]-> (b:Person)
+---------------------+
| a.name | b.name |
+---------------------+
| Kathrine | Riya |
| Kathrine | Lee |
| Lee | Kathrine |
+---------------------+
In the above query:
-[e:knows]->is an edge pattern in whicheis a variable name and:knowsa label expression.- The arrowhead
->specifies that the pattern matches edges that are outgoing fromaand incoming tob.
Label expressions
More complex label expressions are supported through label disjunction. Furthermore, it is possible to omit a label expression.
Label disjunction
The bar operator (|) is a logical OR for specifying that a vertex or edge should match as long as it has either of the specified labels.
For example:

SELECT n.name, n.dob
FROM student_network
MATCH (n:Person|University)
+--------------------------+
| n.name | n.dob |
+--------------------------+
| Riya | 1995-03-20 |
| Kathrine | 1994-01-15 |
| Lee | 1996-01-29 |
| UC Berkeley | <null> |
+--------------------------+
In the query above, (n:Person|University) matches vertices that have either the label Person or the label University. Note that in the result, there is a <null> value in the last row because the corresponding vertex does not have a property dob.
Omitting a label expression
Label expressions may be omitted so that the vertex or edge pattern will then match any vertex or edge.
For example:

SELECT n.name, n.dob
FROM student_network
MATCH (n)
+--------------------------+
| n.name | n.dob |
+--------------------------+
| Riya | 1995-03-20 |
| Kathrine | 1994-01-15 |
| Lee | 1996-01-29 |
| UC Berkeley | <null> |
+--------------------------+
Note that the query gives the same results as before since both patterns (n) and (n:Person|University) match all the vertices in the example graph.
Filter predicates
Filter predicates provide a way to further restrict which vertices or edges may bind to patterns. A filter predicate is a boolean value expression and is placed in a WHERE clause.
For example, “find all persons that have a date of birth (dob) greater than 1995-01-01”:

SELECT n.name, n.dob
FROM student_network
MATCH (n)
WHERE n.dob > DATE '1995-01-01'
+---------------------+
| n.name | n.dob |
+---------------------+
| Riya | 1995-03-20 |
| Lee | 1996-01-29 |
+---------------------+
Above, the vertex pattern (n) initially matches all three Person vertices in the graph as well as the University vertex, since no label expression is specified.
However, the filter predicate n.dob > DATE '1995-01-01' filters out Kathrine because her date of birth is before 1995-01-01.
It also filters out UC Berkeley because the vertex does not have a property dob so that the reference n.dob returns null and since null > DATE '1995-01-01' is null (see three-valued logic) the final result is null, which has the same affect as false and thus this candidate solution gets filtered out.
Another example is to “find people that Kathrine knows and that are old than her”:

SELECT m.name AS name, m.dob AS dob
FROM student_network
MATCH (n) -[e]-> (m)
WHERE n.name = 'Kathrine' AND n.dob <= m.dob
+-------------------+
| name | dob |
+-------------------+
| Riya | 1995-03-20 |
| Lee | 1996-01-29 |
+-------------------+
Here, the pattern (n) -[e]-> (m) initially matches all the edges in the graph since it does not have any label expression.
However, the filter expression n.name = 'Kathrine' AND n.dob <= m.dob specifies that the source of the edge has a property name with the value Kathrine and that both the source and destination of the edge have properties dob such that the value for the source is smaller than or equal to the value for the destination.
Only two out of six edges satisfy this filter predicate.
More complex patterns
More complex patterns are formed either by forming longer path patterns that consist of multiple edge patterns, or by specifying multiple comma-separated path patterns that share one or more vertex variables.
For example, “find people that Lee knows and that are a student at the same university as Lee”:

SELECT p2.name AS friend, u.name AS university
FROM student_network
MATCH (u:University) <-[:studentOf]- (p1:Person) -[:knows]-> (p2:Person) -[:studentOf]-> (u)
WHERE p1.name = 'Lee'
+------------------------+
| friend | university |
+------------------------+
| Kathrine | UC Berkeley |
+------------------------+
Above, in the MATCH clause there is only one path pattern that consists of four vertex patterns and three edge patterns.
Note that the first and last vertex pattern both have the variable u. This means that they are the same variable rather than two different variables. Label expressions may be specified for neither, one, or both of the vertex patterns such that if there are multiple label expressions specified then they are simply evaluated in conjunction such that all expressions need to satisfy for a vertex to bind to the variable.
The same query as above may be expressed through multiple comma-separated path patterns, like this:
SELECT p2.name AS friend, u.name AS university
FROM student_network
MATCH (p1:Person) -[:knows]-> (p2:Person)
, (p1) -[:studentOf]-> (u:University)
, (p2) -[:studentOf]-> (u)
WHERE p1.name = 'Lee'
+------------------------+
| friend | university |
+------------------------+
| Kathrine | UC Berkeley |
+------------------------+
Here again, both occurances of u are the same variable, as well as both occurances of p1 and both occurances of p2.
Binding an element multiple times
In a single solution it is allowed for a vertex or an edge to be bound to multiple variables at the same time.
For example, “find friends of friends of Lee” (friendship being defined by the presence of a ‘knows’ edge):

SELECT p1.name AS p1, p2.name AS p2, p3.name AS p3
FROM student_network
MATCH (p1:Person) -[:knows]-> (p2:Person) -[:knows]-> (p3:Person)
WHERE p1.name = 'Lee'
+-----------------------+
| p1 | p2 | p3 |
+-----------------------+
| Lee | Kathrine | Riya |
| Lee | Kathrine | Lee |
+-----------------------+
Above, in the second solution, Lee is bound to both the variable p1 and the variable p3. This solution is obtained since we can hop from Lee to Kathrine via the edge that is outgoing from Lee, and then we can hop back from Kathrine to Lee via the edge that is incoming to Lee.
If such binding of vertices to multiple variables is not desired, one can use either non-equality constraints or the ALL_DIFFERENT predicate.
For example, the predicate p1 <> p3 in the query below adds the restriction that Lee, which has to bind to variable p1, cannot also bind to variable p3:
SELECT p1.name AS p1, p2.name AS p2, p3.name AS p3
FROM student_network
MATCH (p1:Person) -[:knows]-> (p2:Person) -[:knows]-> (p3:Person)
WHERE p1.name = 'Lee' AND p1 <> p3
+-----------------------+
| p1 | p2 | p3 |
+-----------------------+
| Lee | Kathrine | Riya |
+-----------------------+
An alternative is to use the ALL_DIFFERENT predicate, which can take any number of vertices or edges as input and specifies non-equality between all of them:
SELECT p1.name AS p1, p2.name AS p2, p3.name AS p3
FROM student_network
MATCH (p1:Person) -[:knows]-> (p2:Person) -[:knows]-> (p3:Person)
WHERE p1.name = 'Lee' AND ALL_DIFFERENT(p1, p3)
+-----------------------+
| p1 | p2 | p3 |
+-----------------------+
| Lee | Kathrine | Riya |
+-----------------------+
Besides vertices binding to multiple variables, it is also possible for edges to bind to multiple variables.
For example, “find two people that both know Riya”:
SELECT p1.name AS p1, p2.name AS p2, e1 = e2
FROM student_network
MATCH (p1:Person) -[e1:knows]-> (riya:Person)
, (p2:Person) -[e2:knows]-> (riya)
WHERE riya.name = 'Riya'
+-------------------------------+
| p1 | p2 | e1 = e2 |
+-------------------------------+
| Kathrine | Kathrine | true |
+-------------------------------+
Above, the only solution has Kathrine bound to both variables p1 and p2 and the single edge between Kathrine and Riya is bound to both e1 and e2, which is why e1 = e2 in the SELECT clause returns true.
Again, if such bindings are not desired then one should add constraints like e1 <> e2 or ALL_DIFFERENT(e1, e2) to the WHERE clause.
Matching edges in any direction
Any-directed edge patterns match edges in the graph no matter if they are incoming or outgoing.
An example query with two any-directed edge patterns is:
SELECT *
FROM g MATCH (n) -[e1]- (m) -[e2]- (o)
Note that in case there are both incoming and outgoing data edges between two data vertices, there will be separate result bindings for each of the edges.
Any-directed edge patterns may also be used inside common path expressions:
PATH two_hops AS () -[e1]- () -[e2]- ()
SELECT *
FROM g MATCH (n) -/:two_hops*/-> (m)
The above query will return all pairs of vertices n and m that are reachable via a multiple of two edges, each edge being either an incoming or an outgoing edge.
Main query structure
The previous section on writing simple queries provided a basic introduction to graph pattern matching. The rest of this document introduces the different functionalities in more detail.
The following is the syntax of the main query structure:
Details of the different clauses of a query can be found in the following sections:
- Common Path Expressions allow for specifying complex reachability queries.
- The SELECT clause specifies what should be returned.
- The FROM clause specifies the name of the input graph.
- The MATCH clause specifies the graph pattern that is to be matched.
- The WHERE clause specifies filters.
- The GROUP BY clause allows for creating groups of results.
- The HAVING clause allows for filtering entire groups of results.
- The ORDER BY clause allows for sorting of results.
- The LIMIT and OFFSET clauses allow for pagination of results.
SELECT
In a PGQL query, the SELECT clause defines the data entities to be returned in the result. In other words, the select clause defines the columns of the result table.
The following explains the syntactic structure of SELECT clause.
SelectClause ::= 'SELECT' 'DISTINCT'? ExpAsVar ( ',' ExpAsVar )*
| 'SELECT' '*'
ExpAsVar ::= ValueExpression ( 'AS' VariableName )?
A SELECT clause consists of the keyword SELECT followed by either an optional DISTINCT modifier and comma-separated sequence of ExpAsVar (“expression as variable”) elements, or, a special character star *. An ExpAsVar consists of:
- A
ValueExpression. - An optional
VariableName, specified by appending the keywordASand the name of the variable.
Consider the following example:
SELECT n, m, n.age AS age
FROM g MATCH (n:Person) -[e:friend_of]-> (m:Person)
Per each matched subgraph, the query returns two vertices n and m and the value for property age of vertex n. Note that edge e is omitted from the result even though it is used for describing the pattern.
The DISTINCT modifier allows for filtering out duplicate results. The operation applies to an entire result row, such that rows are only considered duplicates of each other if they contain the same set of values.
Assigning variable name to Select Expression
It is possible to assign a variable name to any of the selection expression, by appending the keyword AS and a variable name. The variable name is used as the column name of the result set. In addition, the variable name can be later used in the ORDER BY clause. See the related section later in this document.
SELECT n.age * 2 - 1 AS pivot, n.name, n
FROM g MATCH (n:Person) -> (m:Car)
ORDER BY pivot
SELECT *
SELECT * is a special SELECT clause. The semantic of SELECT * is to select all the variables in the graph pattern.
Consider the following query:
SELECT *
FROM g MATCH (n:Person) -> (m) -> (w)
, (n) -> (w) -> (m)
This query is semantically equivalent to:
SELECT n, m, w
FROM g MATCH (n:Person) -> (m) -> (w)
, (n) -> (w) -> (m)
SELECT * is not allowed when the graph pattern has zero variables. This is the case when all the vertices and edges in the pattern are anonymous (e.g. MATCH () -> (:Person)).
Futhermore, SELECT * in combination with GROUP BY is not allowed.
FROM
The FROM clause specifies the name of the input graph to be queried:
FromClause ::= 'FROM' GraphName
GraphName ::= IDENTIFIER
For example, the input graph of the following query is my_graph:
SELECT p.first_name, p.last_name
FROM my_graph
MATCH (p:Person)
ORDER BY p.first_name, p.last_name
Default graphs
The FROM clause may be omitted if there is a “default graph” such that specifying the graph name inside the query is only redundant.
PGQL itself does not (yet) provide syntax for specifying a default graph. However, PGQL engines like PGX provide APIs like PgxGraph.queryPgql(..) that provide a default graph (whose name corresponds to PgxGraph.getName()). This in contrast to APIs like PgxSession.queryPgql(..) which do not provide default graphs.
If a default graph is provided then the FROM clause can be omitted from a query like in this example:
SELECT p.first_name, p.last_name
MATCH (p:Person)
ORDER BY p.first_name, p.last_name
MATCH
In a PGQL query, the MATCH clause defines the graph pattern to be matched.
Syntactically, a MATCH clause is composed of the keyword MATCH followed by a comma-separated sequence of path patterns:
MatchClause ::= 'MATCH' GraphPattern
GraphPattern ::= PathPattern ( ',' PathPattern )*
PathPattern ::= SimplePathPattern
| ShortestPathPattern
| TopKShortestPathPattern
SimplePathPattern ::= VertexPattern ( PathPrimary VertexPattern )*
VertexPattern ::= '(' VariableSpecification ')'
PathPrimary ::= EdgePattern
| ReachabilityPathExpression
EdgePattern ::= OutgoingEdgePattern
| IncomingEdgePattern
| AnyDirectedEdgePattern
OutgoingEdgePattern ::= '->'
| '-[' VariableSpecification ']->'
IncomingEdgePattern ::= '<-'
| '<-[' VariableSpecification ']-'
AnyDirectedEdgePattern ::= '-'
| '-[' VariableSpecification ']-'
VariableSpecification ::= VariableName? LabelPredicate?
VariableName ::= IDENTIFIER
A path pattern that describes a partial topology of the subgraph pattern. In other words, a topology constraint describes some connectivity relationships between vertices and edges in the pattern, whereas the whole topology of the pattern is described with one or multiple topology constraints.
A topology constraint is composed of one or more vertices and relations, where a relation is either an edge or a path. In a query, each vertex or edge is (optionally) associated with a variable, which is a symbolic name to reference the vertex or edge in other clauses. For example, consider the following topology constraint:
(n) -[e]-> (m)
The above example defines two vertices (with variable names n and m), and an edge (with variable name e) between them. Also the edge is directed such that the edge e is an outgoing edge from vertex n.
More specifically, a vertex term is written as a variable name inside a pair of parenthesis (). An edge term is written as a variable name inside a square bracket [] with two dashes and an inequality symbol attached to it – which makes it look like an arrow drawn in ASCII art. An edge term is always connected with two vertex terms as for the source and destination vertex of the edge; the source vertex is located at the tail of the ASCII arrow and the destination at the head of the ASCII arrow.
There can be multiple path patterns in the MATCH clause of a PGQL query. Semantically, all constraints are conjunctive – that is, each matched result should satisfy every constraint in the MATCH clause.
Repeated variables
There can be multiple topology constraints in the WHERE clause of a PGQL query. In such a case, vertex terms that have the same variable name correspond to the same vertex entity. For example, consider the following two lines of topology constraints:
(n) -[e1]-> (m1),
(n) -[e2]-> (m2)
Here, the vertex term (n) in the first constraint indeed refers to the same vertex as the vertex term (n) in the second constraint. It is an error, however, if two edge terms have the same variable name, or, if the same variable name is assigned to an edge term as well as to a vertex term in a single query.
Alternatives for specifying graph patterns
There are various ways in which a particular graph pattern can be specified.
First, a single path pattern can be written as a chain of edge terms such that two consecutive edge terms share the common vertex term in between. For example:
(n1) -[e1]-> (n2) -[e2]-> (n3) -[e3]-> (n4)
The above graph pattern is equivalent to the graph pattern specified by the following set of comma-separate path patterns:
(n1) -[e1]-> (n2),
(n2) -[e2]-> (n3),
(n3) -[e3]-> (n4)
Second, it is allowed to reverse the direction of an edge in the pattern, i.e. right-to-left instead of left-to-right. Therefore, the following is a valid graph pattern:
(n1) -[e1]-> (n2) <-[e2]- (n3)
Please mind the edge directions in the above query – vertex n2 is a common outgoing neighbor of both vertex n1 and vertex n3.
Third, it is allowed to ommitg variable names if the particular vertex or edge does not need to be referenced in any of the other clauses (e.g. SELECT or ORDER BY). When the variable name is omitted, the vertex or edge is an “anonymous” vertex or edge.
Syntactically, for vertices, this result in an empty pair of parenthesis. In case of edges, the whole square bracket is omitted in addition to the variable name.
The following table summarizes these short cuts.
| syntax form | example |
|---|---|
| basic form | (n) -[e]-> (m) |
| omit variable name of the source vertex | () -[e]-> (m) |
| omit variable name of the destination vertex | (n) -[e]-> () |
| omit variable names in both vertices | () -[e]-> () |
| omit variable name in edge | (n) -> (m) |
Disconnected graph patterns
In the case the MATCH clause contains two or more disconnected graph patterns (i.e. groups of vertices and relations that are not connected to each other), the different groups are matched independently and the final result is produced by taking the Cartesian product of the result sets of the different groups. The following is an example:
SELECT *
FROM g MATCH (n1) -> (m1), (n2) -> (m2)
Here, vertices n2 and m2 are not connected to vertices n1 and m1, resulting in a Cartesian product.
Label predicates
In the property graph model, vertices and edge may have labels, which are arbitrary (character) strings. Typically, labels are used to encode types of entities. For example, a graph may contain a set of vertices with the label Person, a set of vertices with the label Movie, and, a set of edges with the label likes. A label predicate specifies that a vertex or edge only matches if it has ony of the specified labels. The syntax for specifying a label predicate is through a (:) followed by one or more labels that are separate by a vertical bar (|).
This is explained by the following grammar constructs:
LabelPredicate ::= ':' Label ( '|' Label )*
Label ::= IDENTIFIER
Take the following example:
SELECT *
FROM g MATCH (x:Person) -[e:likes|knows]-> (y:Person)
Here, we specify that vertices x and y have the label Person and that the edge e has the label likes or the label knows.
A label predicate can be specified even when a variable is omitted. For example:
SELECT *
FROM g MATCH (:Person) -[:likes|knows]-> (:Person)
There are also built-in functions available for labels:
- label(element) returns the label of a vertex or edge in the case the vertex/edge has only a single label
- labels(element) returns the set of labels of a vertex or edge in the case the vertex/edge has multiple labels.
- has_label(element, string) returns
trueif the vertex or edge (first argument) has the specified label (second argument).
WHERE
Filters are applied after pattern matching to remove certain solutions. A filter takes the form of a boolean value expression which typically involves certain property values of the vertices and edges in the graph pattern.
The syntax is:
WhereClause ::= 'WHERE' ValueExpression
For example:
SELECT y.name
FROM g MATCH (x) -> (y)
WHERE x.name = 'Jake'
AND y.age > 25
Here, the first filter describes that the vertex x has a property name and its value is Jake. Similarly, the second filter describes that the vertex y has a property age and its value is larger than 25. Here, in the filter, the dot (.) operator is used for property access. For the detailed syntax and semantic of expressions, see Functions and Expressions.
Note that the ordering of constraints does not have an affect on the result, such that query from the previous example is equivalent to:
SELECT y.name
FROM g MATCH (x) -> (y)
WHERE y.age > 25
AND x.name = 'Jake'
Grouping and Aggregation
GROUP BY
GROUP BY allows for grouping of solutions and is typically used in combination with aggregates like MIN and MAX to compute aggregations over groups of solutions.
The following explains the syntactic structure of the GROUP BY clause:
The GROUP BY clause starts with the keywords GROUP BY and is followed by a comma-separated list of value expressions that can be of any type.
Consider the following query:
SELECT n.first_name, COUNT(*), AVG(n.age)
FROM g MATCH (n:Person)
GROUP BY n.first_name
Matches are grouped by their values for n.first_name. For each group, the query selects n.first_name (i.e. the group key), the number of solutions in the group (i.e. COUNT(*)), and the average value of the property age for vertex n (i.e. AVG(n.age)).
Multiple Terms in GROUP BY
It is possible that the GROUP BY clause consists of multiple terms. In such a case, matches are grouped together only if they hold the same result for each of the group expressions.
Consider the following query:
SELECT n.first_name, n.last_name, COUNT(*)
FROM g MATCH (n:Person)
GROUP BY n.first_name, n.last_name
Matches will be grouped together only if they hold the same values for n.first_name and the same values for n.last_name.
Aliases in GROUP BY
Each expression in GROUP BY can have an alias (e.g. GROUP BY n.prop AS myAlias). The alias can be referenced from the HAVING, ORDER BY and SELECT clauses so that repeated specification of the same expression can be avoided.
Note, however, that GROUP BY can also reference aliases from SELECT but it is not allowed to create a circular dependency such that an expression in the SELECT references an expression in the GROUP BY that in its turn references that same expression in the SELECT.
GROUP BY and NULL values
The group for which all the group keys are null is a valid group and takes part in further query processing.
To filter out such a group, use a HAVING clause (see HAVING), for example:
SELECT n.prop1, n.prop2, COUNT(*)
FROM g MATCH (n)
GROUP BY n.prop1, n.prop2
HAVING n.prop1 IS NOT NULL AND n.prop2 IS NOT NULL
Repetition of Group Expression in Select or Order Expression
Group expressions may be repeated in select or order expressions.
Consider the following query:
SELECT n.age, COUNT(*)
FROM g MATCH (n)
GROUP BY n.age
ORDER BY n.age
Here, the group expression n.age is repeated in the SELECT and ORDER BY.
Aggregation
Aggregates COUNT, MIN, MAX, AVG and SUM can aggregate over groups of solutions.
The syntax is:
Aggregation ::= CountAggregation
| MinAggregation
| MaxAggregation
| AvgAggregation
| SumAggregation
| ArrayAggregation
CountAggregation ::= 'COUNT' '(' '*' ')'
| 'COUNT' '(' 'DISTINCT'? ValueExpression ')'
MinAggregation ::= 'MIN' '(' 'DISTINCT'? ValueExpression ')'
MaxAggregation ::= 'MAX' '(' 'DISTINCT'? ValueExpression ')'
AvgAggregation ::= 'AVG' '(' 'DISTINCT'? ValueExpression ')'
SumAggregation ::= 'SUM' '(' 'DISTINCT'? ValueExpression ')'
ArrayAggregation ::= 'ARRAY_AGG' '(' 'DISTINCT'? ValueExpression ')'
Syntactically, an aggregation takes the form of aggregate followed by an optional DISTINCT modifier and a ValueExpression.
The following table gives an overview of the different aggregates and their supported input types.
| aggregate operator | semantic | required input type |
|---|---|---|
COUNT |
counts the number of times the given expression has a bound (i.e. is not null). | any type, including vertex and edge |
MIN |
takes the minimum of the values for the given expression. | numeric, string, boolean, date, time [with time zone], or, timestamp [with time zone] |
MAX |
takes the maximum of the values for the given expression. | numeric, string, boolean, date, time [with time zone], or, timestamp [with time zone] |
SUM |
sums over the values for the given expression. | numeric |
AVG |
takes the average of the values for the given expression. | numeric |
ARRAY_AGG |
constructs an array/list of the values for the given expression. | numeric, string, boolean, date, time [with time zone], or, timestamp [with time zone] |
Aggregation with GROUP BY
If a GROUP BY is specified, aggregations are applied to each individual group of solutions.
For example:
SELECT AVG(m.salary)
FROM g MATCH (m:Person)
GROUP BY m.age
Here, we group people by their age and compute the average salary for each such a group.
Aggregation without GROUP BY
If no GROUP BY is specified, aggregations are applied to the entire set of solutions.
For example:
SELECT AVG(m.salary)
FROM g MATCH (m:Person)
Here, we aggregate over the entire set of vertices with label Person, to compute the average salary.
COUNT(*)
COUNT(*) is a special construct that simply counts the number of solutions without evaluating an expression.
For example:
SELECT COUNT(*)
FROM g MATCH (m:Person)
DISTINCT in aggregation
The DISTINCT modifier specifies that duplicate values should be removed before performing aggregation.
For example:
SELECT AVG(DISTINCT m.age)
FROM g MATCH (m:Person)
Here, we aggregate only over distinct m.age values.
HAVING
The HAVING clause is an optional clause that can be placed after a GROUP BY clause to filter out particular groups of solutions.
The syntax is:
HavingClause ::= 'HAVING' ValueExpression
The value expression needs to be a boolean expression.
For example:
SELECT n.name
FROM g MATCH (n) -[:has_friend]-> (m)
GROUP BY n
HAVING COUNT(m) > 10
This query returns the names of people who have more than 10 friends.
Sorting and Row Limiting
ORDER BY
When there are multiple matched subgraph instances to a given query, in general, the ordering between those instances are not defined; the query execution engine can present the result in any order. Still, the user can specify the ordering between the answers in the result using ORDER BY clause.
The following explains the syntactic structure of ORDER BY clause.
OrderByClause ::= 'ORDER' 'BY' OrderTerm ( ',' OrderTerm )*
OrderTerm ::= ValueExpression ( 'ASC' | 'DESC' )?
The ORDER BY clause starts with the keywords ORDER BY and is followed by comma separated list of order terms. An order term consists of the following parts:
- An expression.
- An optional ASC or DESC decoration to specify that ordering should be ascending or descending.
- If no keyword is given, the default is ascending order.
The following is an example in which the results are ordered by property access n.age in ascending order:
SELECT n.name
FROM g MATCH (n:Person)
ORDER BY n.age ASC
Data types for ORDER BY
A partial ordering for the different data types is defined as follows:
- Numeric values are ordered from small to large.
- String values are ordered lexicographically.
- Boolean values are ordered such that
falsecomes beforetrue. - Datetime values (i.e. dates, times, or timestamps) are ordered such that earlier points in time come before later points in time.
Vertices and edges cannot be ordered directly.
Multiple expressions in ORDER BY
An ORDER BY may contain more than one expression, in which case the expresisons are evaluated from left to right. That is, (n+1)th ordering term is used only for the tie-break rule for n-th ordering term. Note that different expressions can have different ascending or descending decorators.
SELECT f.name
FROM g MATCH (f:Person)
ORDER BY f.age ASC, f.salary DESC
LIMIT and OFFSET
The LIMIT puts an upper bound on the number of solutions returned, whereas the OFFSET specifies the start of the first solution that should be returned.
The following explains the syntactic structure for the LIMIT and OFFSET clauses:
LimitOffsetClauses ::= 'LIMIT' LimitOffsetValue ( 'OFFSET' LimitOffsetValue )?
| 'OFFSET' LimitOffsetValue ( 'LIMIT' LimitOffsetValue )?
LimitOffsetValue ::= UNSIGNED_INTEGER
| BindVariable
The LIMIT clause starts with the keyword LIMIT and is followed by an integer that defines the limit. Similarly, the OFFSET clause starts with the keyword OFFSET and is followed by an integer that defines the offset. Furthermore:
The LIMIT and OFFSET clauses can be defined in either order.
The limit and offset may not be negatives.
The following semantics hold for the LIMIT and OFFSET clauses:
The OFFSET clause is always applied first, even if the LIMIT clause is placed before the OFFSET clause inside the query.
An OFFSET of zero has no effect and gives the same result as if the OFFSET clause was omitted.
If the number of actual solutions after OFFSET is applied is greater than the limit, then at most the limit number of solutions will be returned.
In the following query, the first 5 intermediate solutions are pruned from the result (i.e. OFFSET 5). The next 10 intermediate solutions are returned and become final solutions of the query (i.e. LIMIT 10).
SELECT n
FROM g MATCH (n)
LIMIT 10
OFFSET 5
Variable-Length Paths
Graph Pattern Matching introduced how “fixed-length” patterns can be matched. Fixed-length patterns match a fixed number of vertices and edges such that every solution (every row) has the same number of vertices and edges.
However, through the use of quantifiers (introduced below) it is is possible to match “variable-length” paths such as shortest paths. Variable-length path patterns match a variable number of vertices and edges such that different solutions (different rows) potentially have different numbers of vertices and edges.
Quantifiers
Quantifiers allow for matching variable-length paths by specifying lower and upper limits on the number of times a pattern is allowed to match.
The syntax is:
GraphPatternQuantifier ::= ZeroOrMore
| OneOrMore
| Optional
| ExactlyN
| NOrMore
| BetweenNAndM
| BetweenZeroAndM
ZeroOrMore ::= '*'
OneOrMore ::= '+'
Optional ::= '?'
ExactlyN ::= '{' UNSIGNED_INTEGER '}'
NOrMore ::= '{' UNSIGNED_INTEGER ',' '}'
BetweenNAndM ::= '{' UNSIGNED_INTEGER ',' UNSIGNED_INTEGER '}'
BetweenZeroAndM ::= '{' ',' UNSIGNED_INTEGER '}'
The meaning of the different quantifiers is:
| quantifier | meaning | matches |
|---|---|---|
| * | zero (0) or more | a path that connects the source and destination of the path by zero or more matches of a given pattern |
| + | one (1) or more | a path that connects the source and destination of the path by one or more matches of a given pattern |
| ? | zero or one (1), i.e. “optional” | a path that connects the source and destination of the path by zero or one matches of a given pattern |
| { n } | exactly n | a path that connects the source and destination of the path by exactly n matches of a given pattern |
| { n, } | n or more | a path that connects the source and destination of the path by at least n matches of a given pattern |
| { n, m } | between n and m (inclusive) | a path that connects the source and destination of the path by at least n and at most m (inclusive) matches of a given pattern |
| { , m } | between zero (0) and m (inclusive) | a path that connects the source and destination of the path by at least 0 and at most m (inclusive) matches of a given pattern |
All paths are considered, even the ones that contain a vertex or edge multiple times. In other words, cycles are permitted.
An example is:

SELECT a.number AS a,
b.number AS b,
COUNT(e) AS pathLength,
ARRAY_AGG(e.amount) AS amounts
FROM financial_transactions
MATCH SHORTEST ( (a:Account) -[e:transaction]->* (b:Account) )
WHERE a.number = 10039 AND b.number = 2090
+------------------------------------------------------+
| a | b | pathLength | amounts |
+------------------------------------------------------+
| 10039 | 2090 | 3 | [1000.0, 1500.3, 9999.5] |
+------------------------------------------------------+
Above, we use the quantifier * to find a shortest path from account 10039 to account 2090, following only transaction edges.
Shortest path finding is explained in more detail in Shortest Path. COUNT(e) and ARRAY_AGG(e.amount) are horizontal aggregations which are explained in Horizontal Aggregation.
Horizontal Aggregation
Aggregations are either applied in a vertical or a horizontal fashion.
Recap of vertical aggregation
Vertical aggregation was introduced in Aggregation. This kind of aggregation is what people usually learn first when they start using PGQL or SQL.
Vertical aggregation takes a group of values from different rows and aggregates the values into a single value, for example by taking the minimum or maximum. If a GROUP BY is specified then the output of a query is as many rows as there are groups, while if no GROUP BY is specified then the output is a single row. For more details, see Grouping and Aggregation.
Given the pattern (n) -[e]-> (m), examples of vertical aggregation are:
SUM(e.prop)COUNT(e.prop)SUM(n.prop + m.prop / 2)
Group Variables
To understand horizontal aggregation, however, it is neccesary to know the difference between “singleton variables” and “group variables”. A singleton variable is a variable that binds to only one vertex or edge, whereas a group variable is a variable that may bind to multiple vertices or edges.
Consider the pattern (n) -[e1]-> (m) -[e2]->* (o).
Here, e1 is a singleton variable because within a single match of the pattern there is always a single edge bound to e1, whereas e2 is a group variable because within a single match of the pattern there may be multiple edges bound to e2 because of the quantifier *.
Variables are thus either singleton variables or group variables depending on whether they are enclosed by a quantifier with an upper bound greater than 1.
Here are examples of singleton variables:
-[e]->(or-[e]->{1,1})-[e]->?(or-[e]->{0,1})
Here are examples of group variables:
-[e]->*-[e]->+-[e]->{1,4}
Group variables thus form implicit groups without a need to explicitly specify a GROUP BY.
Horizontal aggregation using group variables
Group variables can be used to perform horizontal aggregation. To be precise, an aggregation is applied in a horizontal manner if the expression that is input to the aggregation contains at least one group variable. The input values for the aggregation are obtained by evaluating the expression once for each binding of the group variable(s) within the particular match. A separate output is generated for each match of the pattern rather than that a single output is generated for an entire group of matches like in case of vertical aggregation.
The same aggregates (MIN, MAX, AVG, etc.) that are used for vertical aggregation are also used for horizontal aggregation.
Given the pattern ( (n) -[e]-> (m) )*, examples of horizontal aggregations are:
SUM(e.prop * 2)COUNT(e.prop)ARRAY_AGG(n.prop)
Aggregations with multiple group variables such as SUM(n.prop + m.prop / 2) are not supported in PGQL 1.2 and are planned for a future version.
It is possible to mix vertical and horizontal aggregation in a single query. For example:

SELECT SUM(COUNT(e)) AS sumOfPathLengths
FROM financial_transactions
MATCH SHORTEST ( (a:Account) -[e:transaction]->* (b:Account) )
WHERE a.number = 10039 AND (b.number = 1001 OR b.number = 2090)
+------------------+
| sumOfPathLengths |
+------------------+
| 5 |
+------------------+
Above, we first match a shortest path between accounts 10039 and 1001. Notice that the length of this path is 2.
We also match a shortest path between accounts 10039 and 2090. Notice that the length of this path is 3.
In the SELECT clause, the aggregation COUNT(e) is a horizontal aggregation since e is a group variable. For each of the two shortest paths, COUNT(e) computes the length by counting the number of edges. The output will be 2 for one of the two paths, and 3 for the other.
Then it takes the SUM to compute the total length of the two paths, which is 5.
Horizontal aggregation in WHERE and GROUP BY
While vertical aggregation is only possible in the SELECT, HAVING and ORDER BY clauses, horizontal aggregation is also possible in the WHERE and GROUP BY clauses.
An example of a horizontal aggregation in WHERE is:

SELECT b.number AS b,
COUNT(e) AS pathLength,
ARRAY_AGG(e.amount) AS transactions
FROM financial_transactions
MATCH SHORTEST ( (a:Account) -[e:transaction]->* (b:Account) )
WHERE a.number = 10039 AND
(b.number = 8021 OR b.number = 1001 OR b.number = 2090) AND
COUNT(e) <= 2
ORDER BY pathLength
+--------------------------------------+
| b | pathLength | transactions |
+--------------------------------------+
| 8021 | 1 | [1000.0] |
| 1001 | 2 | [1000.0, 1500.3] |
+--------------------------------------+
Above, we compute a shortest path from account 10039 to accounts 8021, 1001, and 2090. So three paths in total.
However, in the WHERE clause we only keep paths that have at most two edges (COUNT(e) <= 2) such that only the paths to accounts 8021 and 1001 are kept since the path to 2090 has three edges.
An example of a horizontal aggregation in GROUP BY is:

SELECT COUNT(e) AS pathLength,
COUNT(*) AS cnt
FROM financial_transactions
MATCH SHORTEST ( (a:Account) -[e:transaction]->* (b:Account) )
WHERE (a.number = 10039 OR a.number = 8021) AND
(b.number = 1001 OR b.number = 2090)
GROUP BY COUNT(e)
ORDER BY pathLength
+------------------+
| pathLength | cnt |
+------------------+
| 1 | 1 |
| 2 | 2 |
| 3 | 1 |
+------------------+
Above, we first match shortst paths between four pairs of vertices and then we group by the length of the paths (GROUP BY COUNT(e)) by means of horizontal aggregation. Then we perform a vertical aggregation COUNT(*) to compute the number of paths that have the particular path length. The result shows that one path has length 1, two paths have length 2, and one path as length 3.
Reachability
In graph reachability we test for the existence of paths (true/false) between pairs of vertices. PGQL uses forward slashes (-/ and /->) instead of square brackets (-[ and ]->) to indicate reachability semantic.
The syntax is:
ReachabilityPathExpression ::= OutgoingPathPattern
| IncomingPathPattern
OutgoingPathPattern ::= '-/' PathSpecification '/->'
IncomingPathPattern ::= '<-/' PathSpecification '/-'
PathSpecification ::= LabelPredicate
| PathPredicate
PathPredicate ::= ':' Label GraphPatternQuantifier?
For example:
SELECT c.name
FROM g MATCH (c:Class) -/:subclass_of*/-> (arrayList:Class)
WHERE arrayList.name = 'ArrayList'
Here, we find all classes that are a subclass of 'ArrayList'. The regular path pattern subclass_of* matches a path consisting of zero or more edges with the label subclass_of. Because the pattern may match a path with zero edges, the two query vertices can be bound to the same data vertex if the data vertex satisfies the constraints specified in both source and destination vertices (i.e. the vertex has a label Class and a property name with a value ArrayList).
Examples with various quantifiers
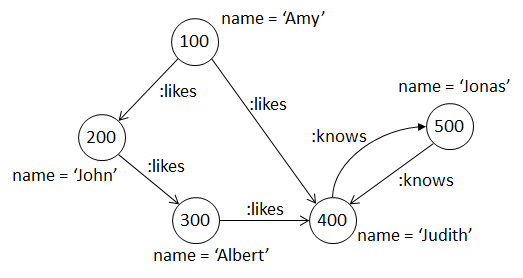
Zero or more
The following example finds all vertices y that can be reached from Amy by following zero or more likes edges.
SELECT y.name
FROM g MATCH (x:Person) -/:likes*/-> (y)
WHERE x.name = 'Amy'
+--------+
| y.name |
+--------+
| Amy |
| John |
| Albert |
| Judith |
+--------+
Note that here, Amy is returned since Amy connects to Amy by following zero likes edges. In other words, there exists an empty path for the vertex pair.
For Judith, there exist two paths (100 -> 200 -> 300 -> 400 and 100 -> 400). However, Judith is still only returned once since the semantic of -/ .. /-> is to test for the existence of paths between pairs of vertices (i.e. “reachability”), so there is only at most one result per pair of vertices.
One or more
The following example finds all people that can be reached from Amy by following one or more likes edges.

SELECT y.name
FROM g MATCH (x:Person) -/:likes+/-> (y)
WHERE x.name = 'Amy'
+--------+
| y.name |
+--------+
| John |
| Albert |
| Judith |
+--------+
This time, Amy is not returned since there does not exist a path that connects Amy to Amy that has a length greater than zero.
The following example finds all people that can be reached from Judith by following one or more knows edges:

SELECT y.name
FROM g MATCH (x:Person) -/:knows+/-> (y)
WHERE x.name = 'Judith'
+--------+
| y.name |
+--------+
| Jonas |
| Judith |
+--------+
Here, in addition to Jonas, Judith is returned since there exist paths from Judith back to Judith that has a length greater than zero. Examples of such paths are 400 -> 500 -> 400 and 400 -> 500 -> 400 -> 500 -> 400.
Optional
The following example finds all people that can be reached from Judith by following zero or one knows edges.

SELECT y.name
FROM g MATCH (x:Person) -/:knows?/-> (y)
WHERE x.name = 'Judith'
+--------+
| y.name |
+--------+
| Judith |
| Jonas |
+--------+
Here, Judith is returned since there exists the empty path that starts in 400 and ends in 400. Jonas is returned because of the following path that has length one: 400 -> 500.
Exactly n
The following example finds all people that can be reached from Amy by following exactly two likes edges.

SELECT y.name
FROM g MATCH (x:Person) -/:likes{2}/-> (y)
WHERE x.name = 'Amy'
+--------+
| y.name |
+--------+
| Albert |
+--------+
Here, Albert is returned since there exists the following path that has likes edges only: 100 -> 200 -> 300.
n or more
The following example finds all people that can be reached from Amy by following 2 or more likes edges.

SELECT y.name
FROM g MATCH (x:Person) -/:likes{2,}/-> (y)
WHERE x.name = 'Amy'
+--------+
| y.name |
+--------+
| Albert |
| Judith |
+--------+
Here, Albert is returned since there exists the following path of length two: 100 -> 200 -> 300. Judith is returned since there exists a path of length three: 100 -> 200 -> 300 -> 400.
Between n and m
The following example finds all people that can be reached from Amy by following between 1 and 2 likes edges.

SELECT y.name
FROM g MATCH (x:Person) -/:likes{1,2}/-> (y)
WHERE x.name = 'Amy'
+--------+
| y.name |
+--------+
| John |
| Albert |
| Judith |
+--------+
Here, John is returned since there exists a path of length one (i.e. 100 -> 200);
Albert is returned since there exists a path of length two (i.e. 100 -> 200 -> 300);
Judith is returned since there exists a path of length one (i.e. 100 -> 400).
Between zero and m
The following example finds all people that can be reached from Judith by following at most 2 knows edges.

SELECT y.name
FROM g MATCH (x:Person) -/:knows{,2}/-> (y)
WHERE x.name = 'Judith'
+--------+
| y.name |
+--------+
| Jonas |
| Judith |
+--------+
Here, Jonas is returned since there exists a path of length one (i.e. 400 -> 500).
For Judith, there exists an empty path of length zero (i.e. 400) as well as a non-empty path of length two (i.e. 400 -> 500 -> 400).
Yet, Judith is only returned once.
Common Path Expressions
One or more “common path expression” may be declared at the beginning of the query. These can be seen as macros that allow for expressing complex regular expressions. PGQL 1.2 allows common path expressions only for reachability, not for (top-k) shortest path.
CommonPathExpressions ::= CommonPathExpression+
CommonPathExpression ::= 'PATH' IDENTIFIER 'AS' PathPattern WhereClause?
A path pattern declaration starts with the keyword PATH, followed by an expression name, the assignment operator AS, and a path pattern consisting of at least one vertex. The syntactic structure of the path pattern is the same as a path pattern in the MATCH clause.
For example:
PATH has_parent AS () -[:has_father|has_mother]-> (:Person)
SELECT ancestor.name
FROM g MATCH (p1:Person) -/:has_parent+/-> (ancestor)
, (p2:Person) -/:has_parent+/-> (ancestor)
WHERE p1.name = 'Mario'
AND p2.name = 'Luigi'
The above query finds common ancestors of Mario and Luigi.
Another example is:
PATH connects_to AS (:Generator) -[:has_connector]-> (c:Connector) <-[:has_connector]- (:Generator)
WHERE c.status = 'OPERATIONAL'
SELECT generatorA.location, generatorB.location
FROM g MATCH (generatorA) -/:connects_to+/-> (generatorB)
The above query outputs all generators that are connected to each other via one or more connectors that are all operational.
Shortest Path
SHORTEST allows for matching a shortest path (i.e. minimal number of edges) between a source vertex and a destination vertex. In case multiple shortest paths exist, an arbitrary one is retrieved.
The syntax is:
ShortestPathPattern ::= 'SHORTEST' '(' SourceVertexPattern
QuantifiedShortestPathPrimary
DestinationVertexPattern ')'
SourceVertexPattern ::= VertexPattern
DestinationVertexPattern ::= VertexPattern
QuantifiedShortestPathPrimary ::= ShortestPathPrimary GraphPatternQuantifier?
ShortestPathPrimary ::= EdgePattern
| ParenthesizedPathPatternExpression
ParenthesizedPathPatternExpression ::= '(' VertexPattern? EdgePattern VertexPattern? WhereClause? ')'
For example:
SELECT src, SUM(e.weight), dst
FROM g
MATCH SHORTEST ( (src) -[e]->* (dst) )
WHERE src.age < dst.age
Another example is:

SELECT COUNT(e) AS num_hops
, p1.name AS start
, ARRAY_AGG ( CASE
WHEN has_label(dst, 'Account')
THEN CAST(dst.number AS STRING)
ELSE dst.name
END
) AS path
FROM financial_transactions
MATCH SHORTEST ( (p1:Person) (-[e]- (dst))* (p2:Person) )
WHERE p1.name = 'Camille' AND p2.name = 'Liam'
ORDER BY num_hops
+------------------------------------------+
| num_hops | start | path |
+------------------------------------------+
| 3 | Camille | [10039, 2090, Liam] |
+------------------------------------------+
Filters on vertices and edges along paths can be specified by adding a WHERE clause inside the quantified pattern.
For example, the following query matches a shortest path (if one exists) such that each edge along the path has a property weight with a value greater than 10:
SELECT src, ARRAY_AGG(e.weight), dst
FROM g
MATCH SHORTEST ( (src) (-[e]-> WHERE e.weight > 10)* (dst) )
Note that this is different from a WHERE clause that is placed outside of the quantified pattern:
SELECT src, ARRAY_AGG(e.weight), dst
FROM g
MATCH SHORTEST ( (src) -[e]->* (dst) ) WHERE SUM(e.cost) < 100
Here, the filter is applied only after a shortest path is matched such that if the WHERE condition is not satisfied, the path is filtered out and no other path is considered even though another path may exist that does satisfy the WHERE condition.
Top-K Shortest Path
TOP k SHORTEST path matches the k shortest paths for each pair of source and destination vertices. Aggregations can then be computed over their vertices/edges.
The syntax is:
TopKShortestPathPattern ::= 'TOP' KValue ShortestPathPattern
KValue ::= UNSIGNED_INTEGER
For example the following query will output the sum of the edge weights along each of the top 3 shortest paths between each of the matched source and destination pairs:
SELECT src, SUM(e.weight), dst
FROM g
MATCH TOP 3 SHORTEST ( (src) -[e]->* (dst) )
WHERE src.age < dst.age
Notice that the sum aggregation is computed for each matching path. In other words, the number of rows returned by the query is equal to the number of paths that match, which is at most three times the number of possible source-destination pairs.
The ARRAY_AGG construct allows users to output properties of edges/vertices along the path. For example, in the following query:
SELECT src, ARRAY_AGG(e.weight), ARRAY_AGG(v1.age), ARRAY_AGG(v2.age), dst
FROM g
MATCH TOP 3 SHORTEST ( (src) ((v1) -[e]-> (v2))* (dst) )
WHERE src.age < dst.age
the ARRAY_AGG(e.weight) outputs a list containing the weight property of all the edges along the path,
the ARRAY_AGG(v1.cost) outputs a list containing the age property of all the vertices along the path except the last one,
the ARRAY_AGG(v2.cost) outputs a list containing the age property of all the vertices along the path except the first one.
Users can also compose shortest path constructs with other matching operators:
SELECT ARRAY_AGG(e1.weight), ARRAY_AGG(e2.weight)
FROM g
MATCH (start) -> (src)
, TOP 3 SHORTEST ( (src) (-[e1]->)* (mid) )
, SHORTEST ( (mid) (-[e2]->)* (dst) )
, (dst) -> (end)
Another example is:

SELECT COUNT(e) AS num_hops
, SUM(e.amount) AS total_amount
, ARRAY_AGG(e.amount) AS amounts_along_path
FROM financial_transactions
MATCH TOP 7 SHORTEST ( (a:Account) -[e:transaction]->* (b:Account) )
WHERE a.number = 10039 AND a = b
ORDER BY num_hops, total_amount
+--------------------------------------------------------------------------------------------+
| num_hops | total_amount | amounts_along_path |
+--------------------------------------------------------------------------------------------+
| 0 | <null> | <null> |
| 4 | 22399.8 | [1000.0, 1500.3, 9999.5, 9900.0] |
| 4 | 23900.2 | [1000.0, 3000.7, 9999.5, 9900.0] |
| 8 | 44799.6 | [1000.0, 1500.3, 9999.5, 9900.0, 1000.0, 1500.3, 9999.5, 9900.0] |
| 8 | 46300.0 | [1000.0, 1500.3, 9999.5, 9900.0, 1000.0, 3000.7, 9999.5, 9900.0] |
| 8 | 46300.0 | [1000.0, 3000.7, 9999.5, 9900.0, 1000.0, 1500.3, 9999.5, 9900.0] |
| 8 | 47800.4 | [1000.0, 3000.7, 9999.5, 9900.0, 1000.0, 3000.7, 9999.5, 9900.0] |
+--------------------------------------------------------------------------------------------+
Note that above, we matched a path with zero edges (the first result) and we also matched four paths (the last four results) that visit the same edges multiple times. The following example shows how such paths could be filtered out, such that we only keep paths that have at least one edge and that do not visit an edge multiple times:

SELECT COUNT(e) AS num_hops
, SUM(e.amount) AS total_amount
, ARRAY_AGG(e.amount) AS amounts_along_path
FROM financial_transactions
MATCH TOP 7 SHORTEST ( (a:Account) -[e:transaction]->* (b:Account) )
WHERE a.number = 10039 AND a = b AND COUNT(DISTINCT e) = COUNT(e) AND COUNT(e) > 0
ORDER BY num_hops, total_amount
+------------------------------------------------------------+
| num_hops | total_amount | amounts_along_path |
+------------------------------------------------------------+
| 4 | 22399.8 | [1000.0, 1500.3, 9999.5, 9900.0] |
| 4 | 23900.2 | [1000.0, 3000.7, 9999.5, 9900.0] |
+------------------------------------------------------------+
Functions and Expressions
Value expressions are used in various parts of the language, for example, to filter solutions (WHERE and HAVING), to project out computed values (SELECT), or, to group by or order by computed values (GROUP BY and ORDER BY).
The following are the relevant grammar rules:
ValueExpression ::= VariableReference
| PropertyAccess
| Literal
| BindVariable
| ArithmeticExpression
| RelationalExpression
| LogicalExpression
| BracketedValueExpression
| FunctionInvocation
| Aggregation
| ExtractFunction
| IsNullPredicate
| IsNotNullPredicate
| CastSpecification
| CaseExpression
| InPredicate
| NotInPredicate
| ExistsPredicate
| ScalarSubquery
VariableReference ::= VariableName
PropertyAccess ::= VariableReference '.' PropertyName
PropertyName ::= IDENTIFIER
BracketedValueExpression ::= '(' ValueExpression ')'
A value expression is one of:
- A variable reference, being either a reference to a
VertexPattern, anEdgePattern, or anExpAsVar. - A property access, which syntactically takes the form of a variable reference, followed by a dot (
.) and the name of a property. - A literal (see Literals).
- A bind variable (see Bind Variables).
- An arithmetic, relational, or logical expression (see Operators).
- A bracketed value expression, which syntactically takes the form of a value expression between rounded brackets. The brackets allow for controlling precedence.
- A function invocation (see String functions, Numeric functions, Datetime functions and Vertex and Edge functions).
- The
IS NULLandIS NOT NULLpredicates (see IS NULL and IS NOT NULL). - The
EXISTSpredicate (see EXISTS and NOT EXISTS subqueries). - An aggregation (see Aggregation).
Data Types and Literals
Data Types
PGQL has the following data types:
STRINGNUMERIC(e.g.INT/INTEGER,LONG,FLOAT,DOUBLE)BOOLEANDATETIMETIMESTAMPTIME WITH TIME ZONETIMESTAMP WITH TIME ZONE
Literals
The syntax is:
Literal ::= StringLiteral
| NumericLiteral
| BooleanLiteral
| DateLiteral
| TimeLiteral
| TimestampLiteral
| TimeWithTimeZoneLiteral
| TimestampWithTimeZoneLiteral
StringLiteral ::= SINGLE_QUOTED_STRING
NumericLiteral ::= UNSIGNED_INTEGER
| UNSIGNED_DECIMAL
BooleanLiteral ::= 'true'
| 'false'
DateLiteral ::= 'DATE' "'" <yyyy-MM-dd> "'"
TimeLiteral ::= 'TIME' "'" <HH:mm:ss> "'"
TimestampLiteral ::= 'TIMESTAMP' "'" <yyyy-MM-dd HH:mm:ss> "'"
TimeWithTimeZoneLiteral ::= 'TIME' "'" <HH:mm:ss+HH:MM> "'"
TimestampWithTimeZoneLiteral ::= 'TIMESTAMP' "'" <yyyy-MM-dd HH:mm:ss+HH:MM> "'"
For example:
| Literal type | Example literal |
|---|---|
| string | 'Clara' |
| integer | 12 |
| decimal | 12.3 |
| boolean | true |
| date | DATE '2017-09-21' |
| time | TIME '16:15:00' |
| timestamp | TIMESTAMP '2017-09-21 16:15:00' |
| time with time zone | TIME '16:15:00+01:00' |
| timestamp with time zone | TIMESTAMP '2017-09-21 16:15:00-03:00' |
Note that according to the grammar rules, numeric literals (integer and decimal) are unsigned. However, signed values can be generated by using the unary minus operator (-).
Bind Variables
In place of a literal, one may specify a bind variable (?). This allows for specifying parameterized queries.
An example query with two bind variables is as follows:
SELECT n.age
FROM g MATCH (n)
WHERE n.name = ?
OR n.age > ?
In the following query, bind variables are used in LIMIT and OFFSET:
SELECT n.name, n.age
FROM g MATCH (n)
ORDER BY n.age
LIMIT ?
OFFSET ?
The following example shows a bind variable in the position of a label:
SELECT n.name
FROM g MATCH (n)
WHERE has_label(n, ?)
Operators
Arithmetic, Relational and Logical Operators
The following table is an overview of the operators:
| operator type | operator |
|---|---|
| arithmetic | +, -, *, /, %, - (unary minus) |
| relational | =, <>, <, >, <=, >= |
| logical | AND, OR, NOT |
The corresponding grammar rules are:
ArithmeticExpression ::= UnaryMinus
| Multiplication
| Division
| Modulo
| Addition
| Subtraction
UnaryMinus ::= '-' ValueExpression
Multiplication ::= ValueExpression '*' ValueExpression
Division ::= ValueExpression '/' ValueExpression
Modulo ::= ValueExpression '%' ValueExpression
Addition ::= ValueExpression '+' ValueExpression
Subtraction ::= ValueExpression '-' ValueExpression
RelationalExpression ::= Equal
| NotEqual
| Greater
| Less
| GreaterOrEqual
| LessOrEqual
Equal ::= ValueExpression '=' ValueExpression
NotEqual ::= ValueExpression '<>' ValueExpression
Greater ::= ValueExpression '>' ValueExpression
Less ::= ValueExpression '<' ValueExpression
GreaterOrEqual ::= ValueExpression '>=' ValueExpression
LessOrEqual ::= ValueExpression '<=' ValueExpression
LogicalExpression ::= Not
| And
| Or
Not ::= 'NOT' ValueExpression
And ::= ValueExpression 'AND' ValueExpression
Or ::= ValueExpression 'OR' ValueExpression
The supported input types and corresponding return types are as follows:
| operator | type of A (and B) | return type |
|---|---|---|
A + BA - BA * BA / BA % B |
numeric | numeric* |
-A (unary minus) |
numeric | type of A |
A = BA <> B |
numeric, string, boolean, date, time [with time zone], timestamp [with time zone], vertex, edge |
boolean |
A < BA > BA <= BA >= B |
numeric, string, boolean, date, time [with time zone], timestamp [with time zone] |
boolean |
NOT AA AND BA OR B |
boolean | boolean |
Binary operations are only allowed if both operands are of the same type, with the following two exceptions:
- time values can be compared to time with time zone values
- timestamp values can be compared to timestamp with time zone values
To compare such time(stamp) with time zone values to other time(stamp) values (with or without time zone), values are first normalized to have the same time zone, before they are compared. Comparison with other operand type combinations, such as dates and timestamp, is not possible. However, it is possible to cast between e.g. dates and timestamps (see CAST).
Operator Precedence
Operator precedences are shown in the following list, from the highest precedence to the lowest. An operator on a higher level (e.g. level 1) is evaluated before an operator on a lower level (e.g. level 2).
| level | operator precedence |
|---|---|
| 1 | - (unary minus) |
| 2 | *, /, % |
| 3 | +, - |
| 4 | =, <>, >, <, >=, <= |
| 5 | NOT |
| 6 | AND |
| 7 | OR |
Implicit Type Conversion
Performing arithmetic operations with different numeric types will lead to implicit type conversion (i.e. coercion).
Coercion is only defined for numeric types. Given a binary arithmetic operation (i.e. +, -, *, /, %), the rules are as follows:
- If both operands are exact numerics (e.g. integer or long), then the result is also an exact numeric with a scale that is at least as large as the scales of each operand.
- If one or both of the operands is approximate numeric (e.g. float, double), the result is an approximate numeric with a scale that is at least as large as the scales of each operand. The precision will also be at least as high as the precision of each operand.
Null values
The property graph data model does not allow properties with null value. Instead, missing or undefined data can be modeled through the absence of properties.
A null value is generated when trying to access a property of a vertex or edge wile the property appears to be missing.
Three-valued logic applies when null values appear in computation.
Three-Valued Logic
An operator returns null if one of its operands yields null, with an exception for AND and OR. This is shown in the following table:
| operator | result when A is null | result when B is null | result when A and B are null |
|---|---|---|---|
A + - * / % B |
null |
null |
null |
- A |
null |
N/A | N/A |
A = <> > < >= <= B |
null |
null |
null |
A AND B |
false if B yields false, null otherwise |
false if A yields false, null otherwise |
null |
A OR B |
true if B yields true, null otherwise |
true if A yields true, null otherwise |
null |
NOT A |
null |
N/A | N/A |
Note that from the table it follows that null = null yields null and not true.
IS NULL and IS NOT NULL
To test whether a value exists or not, one can use the IS NULL and IS NOT NULL constructs.
IsNullPredicate ::= ValueExpression 'IS' 'NULL'
IsNotNullPredicate ::= ValueExpression 'IS' 'NOT' 'NULL'
For example:
SELECT n.name
FROM g MATCH (n)
WHERE n.name IS NOT NULL
Here, we find all the vertices in the graph that have the property name and then return the property.
String functions
JAVA_REGEXP_LIKE
The JAVA_REGEXP_LIKE returns whether the string matches the given Java regular expression pattern.
The syntax is:
JAVA_REGEXP_LIKE( string, pattern )
For example:
JAVA_REGEXP_LIKE('aaaaab', 'a*b')
Result: true
Numeric functions
ABS
The ABS function returns the absolute value of a number. The function returns the same datatype as the numeric datatype of the argument.
The syntax is:
ABS( number )
For example:
ABS(-23)
Result: 23
ABS(-23.6)
Result: 23.6
ABS(-23.65)
Result: 23.65
ABS(23.65)
Result: 23.65
ABS(23.65 * -1)
Result: 23.65
CEIL or CEILING
The CEIL and CEILING functions round the specified number up, and return the smallest number that is greater than or equal to the specified number. The function returns the same datatype as the numeric datatype of the argument.
The syntax is:
CEIL ( number )
CEILING ( number )
For example:
CEIL(3.2)
Result: 4.0
CEIL(2.8)
Result: 3.0
CEIL(3)
Result: 3
FLOOR
The floor function returns the largest integer value that is smaller than or equal to the given argument. The function returns the same datatype as the numeric datatype of the argument.
The syntax is:
FLOOR( number )
For example:
FLOOR(3.2)
Result: 3.0
FLOOR(2.8)
Result: 2.0
FLOOR(3)
Result: 3
ROUND
The round function returns the integer closest to the given argument. The function returns the same datatype as the numeric datatype of the argument.
The syntax is:
ROUND ( number )
For example:
ROUND(3.2)
Result: 3.0
ROUND(2.8)
Result: 3.0
ROUND(3)
Result: 3
Datetime functions
EXTRACT
The EXTRACT function allows for extracting a datetime field, such as a year, month or day, from a datetime value.
The syntax is:
ExtractFunction ::= 'EXTRACT' '(' ExtractField 'FROM' ValueExpression ')'
ExtractField ::= 'YEAR'
| 'MONTH'
| 'DAY'
| 'HOUR'
| 'MINUTE'
| 'SECOND'
| 'TIMEZONE_HOUR'
| 'TIMEZONE_MINUTE'
The fields YEAR, MONTH and DAY can be extracted from a date, a timestamp, or a timestamp with time zone.
For example:
EXTRACT(YEAR FROM DATE '2017-02-13')
Result: 2017
EXTRACT(MONTH FROM DATE '2017-02-13')
Result: 2
EXTRACT(DAY FROM DATE '2017-02-13')
Result: 13
The fields HOUR, MINUTE and SECOND can be extracted from a time, a timestamp, a time with time zone, or a timestamp with time zone.
For example:
EXTRACT(HOUR FROM TIME '12:05:03.201')
Result: 12
EXTRACT(MINUTE FROM TIME '12:05:03.201')
Result: 5
EXTRACT(SECOND FROM TIME '12:05:03.201')
Result: 3.201
The fields TIMEZONE_HOUR and TIMEZONE_MINUTE can be extracted from a time with time zone or a timestamp with time zone.
For example:
EXTRACT(TIMEZONE_HOUR FROM TIMESTAMP '2018-01-01 12:30:00-02:30')
Result: -2
EXTRACT(TIMEZONE_MINUTE FROM TIMESTAMP '2018-01-01 12:30:00-02:30')
Result: -30
Vertex and Edge functions
ID
The ID function returns a system-generated identifier for the vertex/edge (unique within a graph).
The syntax is:
ID( vertex/edge )
LABEL
The LABEL function returns the label of a vertex or an edge. It is an error if the vertex or edge does not have a label, or, has more than one label. The return type of the function is a string.
The syntax is:
LABEL( vertex/edge )
For example:
SELECT LABEL(e)
FROM g MATCH (n:Person) -[e]-> (m:Person)
+----------+
| LABEL(e) |
+----------+
| likes |
| knows |
| likes |
+----------+
LABELS
The LABELS function returns the set of labels of a vertex or an edge. If the vertex or edge does not have a label, an empty set is returned. The return type of the function is a set of strings.
The syntax is:
LABELS( vertex/edge )
For example:
SELECT LABELS(n)
FROM g MATCH (n:Employee|Manager)
+---------------------+
| LABELS(n) |
+---------------------+
| [Employee] |
| [Manager] |
| [Employee, Manager] |
+---------------------+
HAS_LABEL
The HAS_LABEL functions returns true if the vertex or edge (first argument) has the given label (second argument), and false otherwise.
The syntax is:
HAS_LABEL( vertex/edge, string )
ALL_DIFFERENT
The ALL_DIFFERENT function returns true if the provided values are all different from each other, and false otherwise. The function is typically used for specifying that a particular set of vertices or edges are all different from each other. However, the function can be used for values of any data type, as long as the provided values can be compared for equality.
The syntax is:
ALL_DIFFERENT( val1, val2, val3, ..., valN )
For example:
SELECT n.id, m.id, o.id
FROM g MATCH (n) -> (m) -> (o)
WHERE ALL_DIFFERENT( n, m, o )
Note that the above query can be rewritten using non-equality constraints as follows:
SELECT *
FROM g MATCH (n) -> (m) <- (o) -> (n)
WHERE n <> m AND n <> o AND m <> o
Another example is:
ALL_DIFFERENT( 1, 2, 3 )
Result: true
ALL_DIFFERENT( 1, 1.0 )
Result: false
IN_DEGREE
The IN_DEGREE function returns the number of incoming neighbors of a vertex. The return type is an exact numeric.
The syntax is:
IN_DEGREE( vertex )
OUT_DEGREE
The OUT_DEGREE function returns the number of outgoing neighbors of a vertex. The return type is an exact numeric.
The syntax is:
OUT_DEGREE( vertex )
User-Defined functions
User-defined functions (UDFs) are invoked similarly to built-in functions. For example, a user may have registered a function math.tan that returns the tangent of a given angle.
An example invocation of this function is then:
SELECT math.tan(n.angle) AS tangent
FROM g MATCH (n)
ORDER BY tangent
The syntax is:
FunctionInvocation ::= PackageSpecification? FunctionName '(' ArgumentList? ')'
PackageSpecification ::= PackageName '.'
PackageName ::= IDENTIFIER
FunctionName ::= IDENTIFIER
ArgumentList ::= ValueExpression ( ',' ValueExpression )*
Note that a function invocation has an optional package name, a (non-optional) function name, and, zero or more arguments which are arbitrary value expressions.
Function and package names are case-insensitive such that e.g. in_degree(..) is the same as In_Degree(..) or IN_DEGREE(..).
If a UDF is registered that has the same name as a built-in function, then, upon function invocation, the UDF is invoked and not the built-in function. UDFs can thus override built-ins.
CAST
While implicit type conversion is supported between numeric types, between time types, and between timezone types, other type conversions require explicit conversion through casting (CAST).
The syntax is:
CastSpecification ::= 'CAST' '(' ValueExpression 'AS' DataType ')'
DataType ::= 'STRING'
| 'BOOLEAN'
| 'INTEGER'
| 'INT'
| 'LONG'
| 'FLOAT'
| 'DOUBLE'
| 'DATE'
| 'TIME'
| 'TIME WITH TIME ZONE'
| 'TIMESTAMP'
| 'TIMESTAMP WITH TIME ZONE'
For example:
SELECT CAST(n.age AS STRING), CAST('123' AS INTEGER), CAST('09:15:00+01:00' AS TIME WITH TIME ZONE)
FROM g MATCH (n:Person)
Casting is allowed between the following data types:
| from \ to | string | exact numeric | approximate numeric | boolean | time | time with time zone | date | timestamp | timestamp with time zone |
|---|---|---|---|---|---|---|---|---|---|
| string | Y | Y | Y | Y | Y | Y | Y | Y | Y |
| exact numeric | Y | M | M | N | N | N | N | N | N |
| approximate numeric | Y | M | M | N | N | N | N | N | N |
| boolean | Y | N | N | Y | N | N | N | N | N |
| date | Y | N | N | N | N | N | Y | Y | Y |
| time | Y | N | N | N | Y | Y | N | Y | Y |
| timestamp | Y | N | N | N | Y | Y | Y | Y | Y |
| time with time zone | Y | N | N | N | Y | Y | N | Y | Y |
| timestamp with time zone | Y | N | N | N | Y | Y | Y | Y | Y |
In the table above, Y indicates that casting is supported, N indicates that casting is not supported, and M indicates that casting is supported only if the numeric value is between the minimum and maximum values (inclusive) that can be represented by the specified target type.
CASE
The CASE predicate returns an expression based on the evaluation of some given Boolean conditions.
There are two types of CASE expressions: “simple case” and “searched case”.
The syntax is:
CaseExpression ::= SimpleCase | SearchedCase
SimpleCase ::= 'CASE' ValueExpression WhenClause+ ElseClause? 'END'
SearchedCase ::= 'CASE' WhenClause+ ElseClause? 'END'
WhenClause ::= 'WHEN' ValueExpression 'THEN' ValueExpression
ElseClause ::= 'ELSE' ValueExpression
The simple case provides a list of pairs (WHEN compare value, THEN return value) and optionally
an else clause (ELSE return value). PGQL compares a given expression to each compare value and
returns the corresponding return value when compared expressions are equal. If no equal expression
is found and an ELSE clause exists, then PGQL returns the given else value. If no ELSE clause
exists, null is returned.
For example:
CASE n.age
WHEN 1 THEN 'One'
WHEN 2 THEN 'Two'
WHEN 3 THEN 'Three'
ELSE 'Older than three'
END
The searched case provides a list of pairs (WHEN boolean expression, THEN return value) and optionally
an else clause (ELSE return value). PGQL evaluates each boolean expression until one of them evaluates
to true, and returns the corresponding return value. If no expression evaluates to true, and an ELSE
clause exists, then PGQL returns the given else value. If no ELSE clause exists, null is returned.
For example:
CASE
WHEN n.level = 'user' THEN 0
WHEN n.authorized THEN 1
ELSE -1
END
IN and NOT IN
The IN and NOT IN predicates test a value for membership in a list of values.
The PGQL literal types INTEGER, DECIMAL, BOOLEAN, STRING, DATE, TIME [WITH TIME ZONE], TIMESTAMP [WITH TIME ZONE] are allowed in the list.
The syntax is:
InPredicate ::= ValueExpression 'IN' InValueList
NotInPredicate ::= ValueExpression 'NOT' 'IN' InValueList
InValueList ::= '(' ValueExpression ( ',' ValueExpression )* ')'
| BindVariable
For example:
2 IN (2, 3, 5)
Result: true
3.2 IN (5, 4.8, 3.2)
Result: true
false IN (true, true)
Result: false
'Emily' IN ('Emily', 'Carl')
Result: true
DATE '1990-07-03' IN (DATE '1990-07-03', DATE '1993-05-28')
Result: true
TIME '12:00:10' IN (TIME '11:55:10', TIME '06:50:00.999+05:00')
Result: false
TIMESTAMP '2016-03-20 22:09:59.999' IN (TIMESTAMP '2016-03-20 23:09:59')
Result: false
Bind variables are also supported in the position of the list. For example:
SELECT n.date_of_birth
FROM g MATCH (n:Person)
WHERE n.date_of_birth IN ? /* use PreparedStatement.setArray(int, java.util.List) */
Subqueries
There are two types of subqueries:
Both types of subqueries can be used as a value expression in a SELECT, WHERE, GROUP BY, HAVING and ORDER BY clauses (including WHERE clauses of PATH expressions). An EXISTS or NOT EXISTS subquery returns a boolean while a scalar subquery returns a value of any of the supported data types.
EXISTS and NOT EXISTS subqueries
EXISTS returns true/false depending on whether the subquery produces at least one result, given the bindings obtained in the current (outer) query. No additional binding of variables occurs.
The syntax is:
An example is to find friend of friends, and, for each friend of friend, return the number of common friends:
SELECT fof.name, COUNT(friend) AS num_common_friends
FROM g MATCH (p:Person) -[:has_friend]-> (friend:Person) -[:has_friend]-> (fof:Person)
WHERE NOT EXISTS (
SELECT *
FROM g
MATCH (p) -[:has_friend]-> (fof)
)
Here, vertices p and fof are passed from the outer query to the inner query. The EXISTS returns true if there is at least one has_friend edge between vertices p and fof.
Users can add a subquery in the WHERE clause of the PATH definition. One might be interested in asserting for specific properties for a vertex in the PATH. The following example defines a path ending in a vertex which is not the oldest in the graph:
PATH p AS (a) -> (b) WHERE EXISTS ( SELECT * FROM g MATCH (x) WHERE x.age > b.age )
SELECT ...
FROM ...
Topology related constraints can also be imposed. The following example defines a path ending in a vertex which has at least one outgoing edge to some neighbor c:
PATH p AS (a) -> (b) WHERE EXISTS ( SELECT * FROM g MATCH (b) -> (c) )
SELECT ...
FROM ...
Scalar subqueries
Scalar subqueries are queries that return a scalar value (exactly one row and exactly one column) such that they can be part of an expression in a SELECT, WHERE, GROUP BY, HAVING or ORDER BY clause.
The syntax is:
ScalarSubquery ::= Subquery
For example:
SELECT a.name
FROM g MATCH (a)
WHERE a.age > ( SELECT AVG(b.age) FROM g MATCH (a) -[:friendOf]-> (b) )
Another example is:

SELECT p.name AS name
, ( SELECT SUM(t.amount)
FROM financial_transactions
MATCH (a) <-[t:transaction]- (:Account)
) AS sum_incoming
, ( SELECT SUM(t.amount)
FROM financial_transactions
MATCH (a) -[t:transaction]-> (:Account)
) AS sum_outgoing
, ( SELECT COUNT(DISTINCT p2)
FROM financial_transactions
MATCH (a) -[t:transaction]- (:Account) <-[:ownerOf]- (p2:Person)
WHERE p2 <> p
) AS num_persons_transacted_with
, ( SELECT COUNT(DISTINCT c)
FROM financial_transactions
MATCH (a) -[t:transaction]- (:Account) <-[:ownerOf]- (c:Company)
) AS num_companies_transacted_with
FROM financial_transactions
MATCH (p:Person) -[:ownerOf]-> (a:Account)
ORDER BY sum_outgoing + sum_incoming DESC
+-----------------------------------------------------------------------------------------------------+
| name | sum_incoming | sum_outgoing | num_persons_transacted_with | num_companies_transacted_with |
+-----------------------------------------------------------------------------------------------------+
| Liam | 9999.5 | 9900.0 | 1 | 1 |
| Camille | 9900.0 | 1000.0 | 2 | 0 |
| Nikita | 1000.0 | 4501.0 | 1 | 1 |
+-----------------------------------------------------------------------------------------------------+
Note that in the query, the graph name financial_transactions is repeatedly specified. Such repetition may be avoided by relying on a default graph such that the query can be simplified to:
SELECT p.name AS name
, ( SELECT SUM(t.amount)
MATCH (a) <-[t:transaction]- (:Account)
) AS sum_incoming
, ( SELECT SUM(t.amount)
MATCH (a) -[t:transaction]-> (:Account)
) AS sum_outgoing
, ( SELECT COUNT(DISTINCT p2)
MATCH (a) -[t:transaction]- (:Account) <-[:ownerOf]- (p2:Person)
WHERE p2 <> p
) AS num_persons_transacted_with
, ( SELECT COUNT(DISTINCT c)
MATCH (a) -[t:transaction]- (:Account) <-[:ownerOf]- (c:Company)
) AS num_companies_transacted_with
MATCH (p:Person) -[:ownerOf]-> (a:Account)
ORDER BY sum_outgoing + sum_incoming DESC
Other Syntactic rules
Identifiers
Graph names, property names, and labels are all identifiers. These identifiers may either take an unquoted or double quoted form.
Identifiers are used for graph names, property names, and labels. They are either unquoted or double quoted.
The syntax is:
IDENTIFIER ::= UNQUOTED_IDENTIFIER | QUOTED_IDENTIFIER
UNQUOTED_IDENTIFIER ::= [a-zA-Z][a-zA-Z0-9\_]*
QUOTED_IDENTIFIER ::= '"' ( ~[\"\n\\] | ESCAPED_CHARACTER )* '"'
Unquoted identifiers take the form of an alphabetic character followed by zero or more alphanumeric or underscore (i.e. _) characters. Special characters are not supported.
Double quoted identifiers support the full range of Unicode characters.
Special characters in property names, graph names, and labels
Identifiers like graph names, property names, and labels can be delimited with double quotes to allow for encoding of special characters (e.g. the space in the property name n."my prop").
Any Unicode character may be used inside the delimiters.
Lexical constructs for literals
The following are the lexical grammar constructs:
SINGLE_QUOTED_STRING ::= "'" ( ~[\'\n\\] | ESCAPED_CHARACTER )* "'"
UNSIGNED_INTEGER ::= [0-9]+
UNSIGNED_DECIMAL ::= ( [0-9]* '.' [0-9]+ ) | ( [0-9]+ '.' )
These rules describe the following:
- Single quoted strings (used for string literals) consist of:
- A starting single quote.
- Any number of characters that are either:
- Not single quote characters, new line characters, or backslash characters.
- Escaped characters.
- An ending single quote.
- Unsigned integers consist of one or more digits.
- Unsigned decimals consist of zero or more digits followed by a dot (
.) and one or more digits, or, one or more digits followed by only a dot (.).
Escaped characters
Escaping in string literals and identifiers is necessary to support white space, quotation marks, and backslash characters.
The syntax is:
Note that an escaped character is either a tab (\t), a line feed (\n), a carriage return (\r), a single (\') or double quote (\"), or a backslash (\\). Corresponding Unicode code points are shown in the table below.
| escaped character | unicode code point |
|---|---|
\t |
U+0009 (tab) |
\n |
U+000A (line feed) |
\r |
U+000D (carriage return) |
\" |
U+0022 (quotation mark, double quote mark) |
\' |
U+0027 (apostrophe-quote, single quote mark) |
\\ |
U+005C (backslash) |
In string literals, it is optional to escape double quotes.
For example:
'abc\"d\"efg' = 'abc"d"efg'
Result: true
Similarly, in identifiers it is optional to escape single quotes.
In addition to Java-like escaping, string literals in PGQL queries can be escaped in a SQL-like fashion by repeating the quote.
For example, n.prop = 'string''value' is an alternative for n.prop = 'string\'value', and FROM "my""graph" is an alternative for FROM "my\"graph".
Keywords
The following is a list of keywords in PGQL.
PATH, SELECT, FROM, MATCH, WHERE, GROUP, BY,
HAVING, ORDER, ASC, DESC, LIMIT, OFFSET,
AND, OR, NOT, true, false, IS, NULL, AS,
DATE, TIME, TIMESTAMP, WITH, ZONE, DISTINCT,
COUNT, MIN, MAX, AVG, SUM, ARRAY_AGG, IN,
EXISTS, CAST, CASE, WHEN, THEN, ELSE, END,
EXTRACT, YEAR, MONTH, DAY, HOUR, MINUTE,
SECOND, TIMEZONE_HOUR, TIMEZONE_MINUTE,
TOP, SHORTEST
Keywords are case-insensitive and variations such as SELECT, Select and sELeCt can be used interchangeably.
Comments
Comments are delimited by /* and */.
The syntax is:
For example:
/* This is a
multi-line
comment. */
SELECT n.name, n.age
FROM g MATCH (n:Person) /* this is a single-line comment */